Three points on straight line or not

Posted on June 16, 2020

C program to check if all the three points fall on one straight line or not.

Three points when lie on the same line are said to be collinear points. Collinearity of the points can be checked using various methods.

Method 1:
The three points A, B and C are collinear, if the sum of the lengths of any two line segments among AB, BC and AC is equal to the length of the remaining line segment.

Method 2:
Three points are collinear if slope of any two pairs of points is same.

Method 3:
If three points, A, B and C are collinear, they will lie on the same line and they cannot form a triangle.
So, the area of triangle ABC = 0.

Program 

#include<stdio.h>
#include<conio.h>
#include<math.h>
void main()
{
   int x1, y1, x2, y2, x3, y3;
    float ab, bc, ca;

    printf("Enter the x and y coordinates of first point (A)\t:");
    scanf("%d%d",&x1,&y1);
    printf("Enter the x and y coordinates of second point (B)\t:");
    scanf("%d%d",&x2,&y2);
    printf("Enter the x and y coordinates of third point (C)\t:");
    scanf("%d%d",&x3,&y3);

    ab = sqrt((x2-x1)*(x2-x1) + (y2-y1)*(y2-y1));
    bc = sqrt((x3-x2)*(x3-x2) + (y3-y2)*(y3-y2));
    ca = sqrt((x3-x1)*(x3-x1) + (y3-y1)*(y3-y1));

    if((ab==bc+ca) || (bc==ca+ab) || (ca==ab+bc))
		printf("\nThe three points are collinear");
    else
		printf("\nThe three points are not collinear");

    getch();
}

Output 

********** Run1 **********
Enter the x and y coordinates of first point (A)        :1
1
Enter the x and y coordinates of second point (B)       :3
3
Enter the x and y coordinates of third point (C)        :5
5

The three points are collinear


********** Run2 **********
Enter the x and y coordinates of first point (A)        :1
1
Enter the x and y coordinates of second point (B)       :3
4
Enter the x and y coordinates of third point (C)        :6
7

The three points are not collinear

Explanation

Let A, B and C be the three points. We have to find the three lengths AB, BC and AC among the given three points A, B and C.
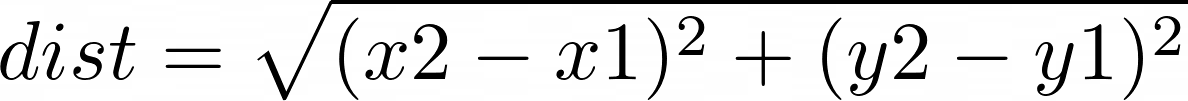
The three points A, B and C are collinear, if the sum of the lengths of any two line segments among AB, BC and AC is equal to the length of the remaining line segment.
i.e. AB + BC = AC (or) AB + AC = BC (or) AC + BC = AB

distance between two points A(x1,y1) and B(x2,y2) is calculated using the following formula



Program 

#include<stdio.h>
#include<conio.h>
#include<stdlib.h>
void main()
{
    int x1, y1, x2, y2, x3, y3;
    float slope1, slope2, slope3;

    printf("Enter the x and y coordinate of first point\t:");
    scanf("%d%d",&x1,&y1);
    printf("Enter the x and y coordinate of second point\t:");
    scanf("%d%d",&x2,&y2);
    printf("Enter the x and y coordinate of third point\t:");
    scanf("%d%d",&x3,&y3);

    slope1 = abs(y2-y1)/abs(x2-x1);
    slope2 = abs(y3-y2)/abs(x3-x2);
    slope3 = abs(y3-y1)/abs(y3-y1);

    if(slope1==slope2 && slope2==slope3)
		printf("\nThe three points are collinear");
    else
		printf("\nThe three points are not collinear");

    getch();
}

Output 

********** Run1 **********
Enter the x and y coordinates of first point (A)        :1
1
Enter the x and y coordinates of second point (B)       :3
3
Enter the x and y coordinates of third point (C)        :5
5

The three points are collinear


********** Run2 **********
Enter the x and y coordinates of first point (A)        :1
1
Enter the x and y coordinates of second point (B)       :3
4
Enter the x and y coordinates of third point (C)        :6
7

The three points are not collinear

Explanation

Three points are collinear if slope of any two pairs of points is same. With three points A, B and C, three pairs of points can be formed, they are: AB, BC and AC.
If Slope of AB = slope of BC = slope of AC, then A, B and C are collinear points.

slope of the line between two points A(x1,y1) and B(x2,y2) is calculated using the following formula
slope = (y2-y1) / (x2-x1)

Program 

#include<stdio.h>
#include<conio.h>
#include<math.h>
void main()
{
    int x1, y1, x2, y2, x3, y3;
    int area;

    printf("Enter the x and y coordinate of first point\t:");
    scanf("%d%d",&x1,&y1);
    printf("Enter the x and y coordinate of second point\t:");
    scanf("%d%d",&x2,&y2);
    printf("Enter the x and y coordinate of third point\t:");
    scanf("%d%d",&x3,&y3);

    area = x1*(y2-y3) + x2*(y3-y1) + x3*(y1-y2);

    if(area == 0)
		printf("\nThe three points are collinear");
    else
		printf("\nThe three points are not collinear");

    getch();
}

Output 

********** Run1 **********
Enter the x and y coordinates of first point (A)        :1
1
Enter the x and y coordinates of second point (B)       :3
3
Enter the x and y coordinates of third point (C)        :5
5

The three points are collinear


********** Run2 **********
Enter the x and y coordinates of first point (A)        :1
1
Enter the x and y coordinates of second point (B)       :3
4
Enter the x and y coordinates of third point (C)        :6
7

The three points are not collinear

Explanation

Let A(x1,y1), B(x2,y2) and C(x3,y3) be the three points. If the three points, A, B and C are collinear, they will lie on the same line and they cannot form a triangle.
So, the area of triangle ABC = 0.
So, we will check if the area formed by the triangle is zero or not.
If the area is zero, then the points are collinear.
else, the points will not be collinear.

Area of triangle ABC = 0.5(x1(y2-y3) + x2(y3-y1) + x3(y1-y2))

condition to be checked is
0.5(x1(y2-y3) + x2(y3-y1) + x3(y1-y2)) == 0
or, x1(y2-y3) + x2(y3-y1) + x3(y1-y2) == 0